Que son las Matrices en Java (Arreglos Bidimensionales)

En una entrada anterior hablamos sobre los Arreglos unidimensionales, en esta ocasión vamos a continuar con la entrada pero ahora conociendo las Matrices o arreglos bidimensionales!!!!

   
¿Que son?

Este tipo de arreglos son conocidos como matrices y corresponden a una estructura de datos que puede almacenar muchos más datos que los arreglos unidimensionales, pues estos últimos como ya se mencionó se componen de una fila por n columnas, mientras que los bidimensionales se componen de n filas por m columnas.

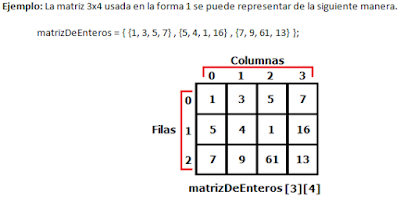
Como se ve en la imagen, se tiene un arreglo de 3 filas por 4 columnas siendo n=3 y m=4, la lógica de la estructura es muy similar a los arreglos unidimensionales, cada índice inicia en 0 hasta el tamaño-1 por esa razón las posiciones de las filas van de 0 a 2 y el de las columnas de 0 a 3.

Se puede ver que la matriz anterior es como si fueran 3 arreglos de tamaño 4 juntos, pues se puede entender cada fila como uno de ellos, por lo tanto la declaración, construcción e inicialización es muy similar.

Declaración de Matrices.

Las matrices se identifican porque al momento de su creación se utilizan doble corchetes ( [ ] [ ]), al usarlos java automáticamente identifica que se va a trabajar con matrices, ya que representan el tamaño de filas por columnas que puede tener, igual que los arreglos unidimensionales se tienen 2 formas generales para su creación.

              <tipoDato>  identificador[ ] [ ];           Ej:  int matrizDeEnteros[ ] [ ];

O también

              <tipoDato>[ ] [ ]  identificador;         Ej:  int[ ] [ ] matrizDeEnteros;

Donde tipo de dato define el tipo de dato de cada uno de los valores que puede contener la matriz.

Construcción de la Matriz.

Después de haber declarado la matriz se puede construir e inicializar de 2 maneras.

Forma1.
la primera se usa cuando inicialmente no sabemos cuáles son los valores que va a contener la matriz, ya que luego serán ingresados, se crea con la siguiente estructura:
 
Identificador = new <tipoDato> [filas] [columnas];       Ej. matrizDeEnteros = new int[3] [4];

Podemos observar como la matrizDeEnteros declarada previamente, ahora es creada con un tamaño de 3 x 4 (3 filas 4 columnas) creándose un total de posiciones de memoria equivalente a la multiplicación de estos valores, así estas posiciones corresponden a un espacio donde se pueden almacenar 12 datos de tipo int.

Inicialización de la Matriz.

Igual que con los arreglos, se deben tener presente el tamaño asignado para las filas y columnas pues cada posición almacenará un valor del tipo de dato declarado para la matriz, el llenado se realiza de la siguiente manera:

          identificador[fila] [columna]=dato;          

Sabemos que el identificador corresponde al nombre de la matriz, posición a alguna de las casillas y dato el valor a asignar, que debe ser del tipo de dato definido al momento de la creación.

Forma 2.
De la misma manera que la segunda forma de llenado de arreglos, para las matrices se usa cuando sabemos con exactitud cuáles son los valores que va a contener la matriz, aquí el proceso de construcción e inicialización se hace directo y se realiza de la siguiente manera:
 
Identificador = { {valor, valor,valor}, {valor, valor,valor}, {valor, valor,valor} };

Dónde:
Identificador: nombre de la matriz
Llaves externas: representa toda la matriz en general
Llaves internas: representan cada una de las filas que puede contener la matriz
Valores: representan los valores de cada columna en la fila respectiva

Como vemos en la estructura, se está creando una matriz de 3x3, pues hay 9 valores repartidos en 3 grupos correspondientes a las filas los cuales se muestran encerrados en las llaves internas.

Como se puede observar no fue necesario indicar cuál es el tamaño de la matriz, ya que java identifica el tamaño gracias a las posiciones y cantidad de valores separados por coma. 

Acceso a los datos de una matriz.

Para acceder a la información almacenada dentro de una matriz se debe tener presente el nombre de la matriz, tamaño y el tipo de datos que contiene.

Por ejemplo, si queremos almacenar un dato de una variable, la forma de acceder es por medio de los  índices de fila y columna que corresponde a la posición del valor a obtener:

             variable = Identificador[fila] [columna];

donde la variable corresponde a una variable del tipo de dato que se quiere almacenar, el identificador corresponde al nombre de la matriz y la posición a alguno de los valores entre 0 y tamaño-1 (tanto para fila como para la columna)

Tomando el ejemplo de la matriz anterior, queremos obtener el valor en la posición (2,3) de la matriz (ver imagen anterior).

Entonces:

           int dato= matrizDeEnteros [2] [3];

Por lo tanto dato, almacenará el valor 16.

Ejemplo Forma 1.
 
Ejemplo Forma 2.

 Ahora miremos el siguiente ejemplo donde se creará la misma matriz anterior pero usando la segunda forma trabajada.

Llenado y consulta de datos del arreglo por medio de ciclos.

Cuando se desea llenar un arreglo de muchas posiciones, los ciclos juegan un papel muy importante ya que nos permitirán hacer este proceso más dinámico, pues podemos recorrer cada posición usando la variable de incremento, tanto para asignar como para obtener.

Teniendo en cuenta que siempre cuando asignamos o consultamos datos del arreglo, debemos indicar cuál es la posición o índice que vamos a usar, la posición podemos trabajarla como una variable que toma  cada uno de los valores posibles que a  tomar.

Ej: arreglo[posición]=valor  //asignación valor en el arreglo
      Variable=  arreglo[posición] //asignación valor del arreglo en la variable.

El ejemplo anterior realiza un proceso similar al llenado y búsqueda de un arreglo, esta vez note que se utilizan 2 ciclos anidados tanto para el llenado como la consulta de los datos.

El primer ciclo for lo que hace es recorrer cada una de las filas, caso contrario el segundo recorre las columnas, de este modo se puede usar el proceso matriz[i][j] para ir almacenando los datos en cada posición dado el vector (i,j) que representa (filas,columnas).

Te comparto este video adicional donde complementas lo visto en esta entrada...

 


También te podría Interesar.

• Que son los arreglos en Java.
• Que son las convenciones de Código en Java 
• Como Importar Proyectos Eclipse en Netbeans
• Redimensionar imagen en Java
• Componentes de Texto.
• Componentes Atomicos Java Swing
• Componentes Java Swing
• Que es Java Swing?
• Instalación del servidor de aplicaciones JBoss 
• Instalación Apache ANT 
• Conceptos Básicos de Programación Orientada a Objetos.

¿Hay algo que quieras anexar o comentar sobre esta entrada?  no dudes en hacerlo.....y si te gustó...... te invito a compartir y Suscribirte ingresando al botón "Participar en este sitio" para darte cuenta de mas entradas como esta ;)